Next: 33.4 CLUSTER Up: 33. Seismic risk related Previous: 33.2 CRISIS2012 Contents Index
The Seisan Explorer functions which are specifically relevant for seismic hazard assessment are described in the following. The user is referred to the separate section on Seisan Explorer for details on the general use of the program.
Function 'Gutenberg-Richter relation' allows for determining a- and b-values of the Gutenberg-Richter relation for a given catalog using different magnitude intervals and bin sizes. The Gutenberg-Richter relation states that
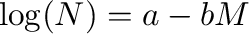 |
(33.1) |
where log is the base-10 logarithm and N is the number of events with magnitude M (or larger in case of regression on cumulative data, see below).
The user can choose which magnitude type to use (M is the first magnitude given for each event ). The database is read, and a histogram is plotted showing the number of events in different magnitude bins. The minimum magnitude to be considered and the bin size can be chosen by the user. Optionally, the incremental number of events and the cumulative number of events above a given magnitude can be overlain as symbols. The a- and b-values can be determined by regression on either the incremental or the cumulative values. The starting magnitude is selected by the user and should be set such that only the complete part of the catalog is considered. It is also possible to set a maximum magnitude in the regression. The obtained a- and b-values are returned, and the fit is compared to the data in the plot.
Function 'Poisson distribution' allows for visually checking whether an earthquake catalog is Poisson distributed. The function reads the database and plots a histogram showing the number of 1-year intervals with a given number of earthquakes, as a function of the annual number of earthquakes. This histogram is compared to the theoretical Poisson distribution derived from
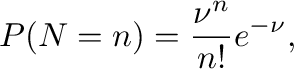
where n is the number of earthquakes for a given year and
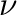 is the mean annual number of events. A good fit between the histogram and the theoretical curve indicates that the data fulfills the Poisson distribution.
is the mean annual number of events. A good fit between the histogram and the theoretical curve indicates that the data fulfills the Poisson distribution.
Function 'Completeness check' allows for defining catalog completeness for different magnitude classes. The function provides a 'staircase plot' of the earthquake catalog, showing for different magnitude classes the cumulative number of events as a function of time. Assuming that the catalog is complete during the most recent part of the time interval, the user can search for a change in slope, indicating a change in seismicity rate. Such change is interpreted as a change in catalog completeness. The completeness time can thus be read as the time where the staircase plot changes slope for a given magnitude class and entered into a table. The plot can be zoomed by scrolling and moved by dragging with the mouse. The user can select the minimum magnitude to be considered and the magnitude interval for each curve. The entered completeness values are shown in the plot and saved to a file se-completeness.out, to be read by function 'Weichert method', when pushing 'Replot'.
Function 'Weichert method' allows for determining a- and b-values for a given catalog, accounting for varying catalog completeness for different magnitude classes following Weichert [1980]. The magnitude classes and their corresponding completeness times are read from the file se-completeness.out, which is generated by function 'Completeness check'. The user can choose which magnitude classes to consider through 'Select intervals to be used'. The function performs a standard linear regression for the Gutenberg-Richter a- and b-values for the complete part of the catalog. In addition, a regression is performed following Weichert [1980]. This regression returns the b-value, the Mmin value used and a value of Ny(M) for a magnitude selected by the user, defined through:
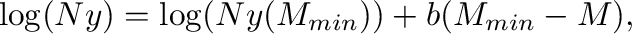 |
(33.2) |
where log is the base-10 logarithm and Ny(M) is the annual number of earthquakes with magnitude M.
Peter Voss : Tue Jun 8 13:38:42 UTC 2021