Next: 28. Merge events in Up: 27. Calculation of coda Previous: 27.4 Program QSTAT Contents Index
Q as a function of frequency is usually described as
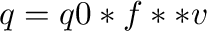
If several such relations are to be averaged, it is not just a question of averaging the parameters. In program AVQ, the averaging is done in the following way:
-For each relation, 1/Q is calculated at the frequencies 1, 2, 4, 8 and 16 Hz.
-At each frequency, average 1/Q is calculated using the number of observations in the original determination of Q for a particular relation as weight.
-A new least squares determination of
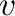 in
in
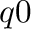 is made with the Q-values.
is made with the Q-values.
The program uses an input file with q0, v and number of observations, one relation (free format) per line. An example of a run is seen below:
C:\seismo\wor>avq File name, enter for automag_grid.out input.txt Q0,alpha,n 100.000000 0.500000000 100 Q0,alpha,n 150.000000 0.300000012 50 Q0,alpha,n 200.000000 0.200000003 10 Q0,alpha,n 170.000000 0.400000006 22 Q0,alpha,n 250.000000 0.150000006 5 Q0,alpha,n 80.0000000 0.800000012 10 Number of curves to average: 6 Running average over how many, enter for average of all? Q0,alpha,corr 119.819160 0.437137932 0.999868274 Output of plot in avq.eps
and the plot seen in figure 27.4 comes up.
![\begin{figure}
\centerline{\includegraphics[width=0.9\linewidth]{fig/avq}}
\end{figure}](img166.png) |
The program also has a special input to be used with AUTOMAG, which can output Q-relations found by grid search, see AUTOMAG for more details. These relations can be averaged over a number of relations. However, here that option is not used.
Peter Voss : Tue Jun 8 13:38:42 UTC 2021