Next: 23.1.2 Automatic reading of Up: 23.1 FOCMEC Previous: 23.1 FOCMEC Contents Index
Amplitude ratios are computed from amplitude readings given in the S-file. While amplitude ratios can provide additional constraint on the solution, they should be used with caution. Ideally, the solution should be well constrained by polarities only, and then amplitude ratios can provide confirmation of a solution or help to select one of several equally good solutions. The principle behind the amplitude ratio method is that the effect of geometrical spreading will cancel out when forming the amplitude ratios of S and P waves (or SV/SH) of the same phase type, e.g. Pg and Sg. This leaves the following corrections to be made on the amplitudes before the ratios are calculated.
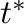 . Different
. Different 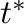 for P and S can be used. The frequency used is the frequency of the maximum amplitude phase.
for P and S can be used. The frequency used is the frequency of the maximum amplitude phase.
Different values can be set in file FOCMEC.DEF, which can be located in DAT or working directory.
If there is no definition of Q in FOCMEC.DEF or the file is not there then the attenuation parameters have default values of:
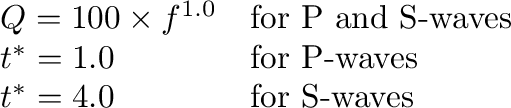
For amplitudes, a model and vpvs are needed. They are dfined in STATION0.HYP.
The observations to be made are:
The wave type Pg/Sg or Pn/Sn has to be given when the amplitude is read. When reading on uncorrected seismograms, MULPLT will want a confirmation that the user wants to save uncorrected amplitudes, since, normally, all amplitude observations in an S-file are in nm. It is possible to filter the signals provided the same filter is used for P and S. Ideally, the amplitude observation should be made at a frequency below the earthquake corner frequency and consequently also the filter high cut frequency should be below the corner frequency.
It is also possible to read amplitudes on the radial component. However, SV amplitudes and phases change rapidly around the critical angle and the amplitudes can therefore be unreliable (see INF/focmec.pdf for details). So, although SEISAN will use the amplitudes read on the radial component, it is in general not recommended to use them. Assuming reading on only Z and H, the following amplitude ratios are calculated:
In reality, the data only provides 2 independent ratios so ideally only 2 should be used. Since it is hard to know which 2 are the most reliable, SEISAN uses all.
The most reliable amplitudes are P on Z and SH on T so if enough data is available, try not to use SV. However, if only Z-channels are available, SV on Z has to be used.
Unwanted amplitudes can be weighted out with wight 4 in S-file.
FOCMEC also uses polarities on S-waves but this has not been implemented in SEISAN since S-polarities seldom are seen clearly. However, they cab be used by editing the focmec.dat file.
Phase names in SEISAN used for amplitudes for FOCMEC have the names AMPG, AMSG, AMPN and AMSN for direct and first arrival (refracted), respectively. For local earthquakes both PG and PN types can be used while for distant earthquakes only PN types can be used.
Peter Voss : Tue Jun 8 13:38:42 UTC 2021